Докозательство:
 |
ДАНО:
Прямолинейная фигура, состоящая из трех прямых а,
b,
с.
А -
точка пересечения прямых а и с.
В - точка пересечения прямых
b
и
с.
α,
β
- внутренние
односторонние углы, при пересечении прямой
c
с
прямыми а║b.
α + β +γ
= 2d.
γ
=
ðΜΡΝ.
α
+
β
< 2d
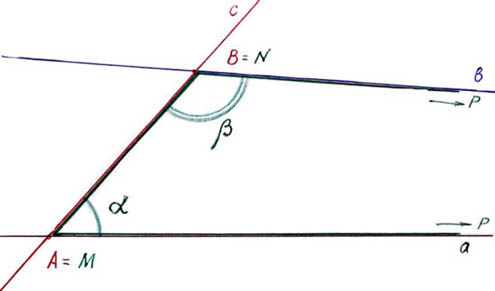
(см. рис.)
ТРЕБУЕТСЯ ДОКАЗАТЬ:
Прямые а и
b
при неограниченном продолжении пересекутся с той стороны, с которой
α + β
< 2d.
ДОКАЗАТЕЛЬСТВО:
Треугольник является жёсткой фигурой. Значит, все треугольники со
стороной, равной АВ (расстояние от точек А и В -
пересечения прямой с с прямыми
a
и
b
) и прилежащими углами
α
и
β
равны между собой. Обозначим один из таких
треугольников
ΔΜΝΡ,
в
котором:
ΜΝ = ΑΒ;
ðΡΜΝ
=
α;
ðΡΝΜ
=
β.
Третий угол
ΔΜΝΡ
составляет:
ðΜΡΝ
= 2d-(α
+
β),
т.к.
сумма углов любого треугольника равна двум прямым углам, т.е.
α + β +γ
= 2d, где
γ =
ðΜΡΝ
в
треугольнике
MNP.
Вложим
ΔΜΝΡ
в
прямолинейную фигуру, состоящую из трёх прямых
a,
b
и с (см. рис.) так, чтобы сторона
MN
совместилась с отрезком АВ, т.е. точка
Μ
совместилась с точкой
A; точка N совместилась с точкой В.
Это возможно, т.к.
ΜΝ =
АВ
по условию выбора
ΔΜΝΡ.
Кроме того,
ðΡΜN
=
α
и
ðΡΝΜ
=
β
расположим по одну сторону с углами
α
и
β
прямолинейной фигуры.
В результате указанного построения:
- прямая с прямолинейной фигуры проходит по стороне
ΜΝ
треугольника
ΜΝΡ,
т.е.
ΜΝ
╠
с;
- прямая а прямолинейной фигуры проходит по стороне
МР треугольника
ΜΝΡ,
т.е. МР
╠
а;
- прямая
b
прямолинейной фигуры проходит по стороне
NP
треугольника
MNP,
т.е.
NP
╠
b
(см. рис.)
Стороны
ΜΡ
и
NP
треугольника
MNP
пересекаются в точке
Ρ
- третья вершина
ΔΜΝΡ.
При
указанных соотношениях стороны
ΜΝ
и двух
прилежащих углов
ðΡΜΝ
=
α,
ðΡΝΜ
=
β
вершина
Ρ
треугольника
ΜΝΡ
единственная, и расположена с той стороны с которой
α +
β
=2d
û
ðΜΡΝ,
или
α
+
β
= 2d
û
γ.
Так как стороны МР и
NP
треугольника
MNP
лежат на прямых а и
b
соответственно, и содержат общую точку Р, то прямые а
и
b
пересекаются в этой же точке Р. Итак,
ΔΜΝΡ
у
которого
MN
=
AB,
ðΡΜΝ
= α,
ðΡΝΜ
=
β
совмещается с "внутренней частью" прямолинейной фигуры, состоящей
из трёх прямых
a,
b
и
с, т е. вершины
Μ, Ν,
Ρ
этого треугольника
ΜΝΡ
совпадают с точками соответственно
A,
В,
и
Ρ
пересечения прямых а и с;
b
и
с; а и b.
ДОКАЗАНО:
что если сумма двух внутренних односторонних углов (α и
β),
двух прямых (а и
b),
пересечённых третьей (с), меньше двух прямых углов (а +
β
< 2d),
то такие прямые (а и
b)
при
достаточном продолжении пересекутся с той стороны секущей (с),
с которой сумма углов меньше 2d.
Угол при пересечении а и
b
в точке
Ρ
составит
γ = 2d-(α+
β).
в начало |



